What is the sum of exterior angles formula? Θ = 360 / 6. the sum of the exterior angles of a hexagon.
The Sum Of The Exterior Angles Of A Hexagon, The sum of the exterior angles is 360 deg, hence each exterior angle is 360/6 = 60. The sum of all the exterior angles of the regular polygon = 360° let the number of sides be = n. In a regular hexagon, all sides are same size and measure of all interior angles are same.
 Interior Angles Of A Hexagon Home Designs From jyden1.com
The sum of interior angles of a hexagon is 720^∘, which is double the sum of exterior angles. Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. From the above triangle, the exterior angle y and r comprise a linear pair.(y + r = 180°).
Because the sum of these angles will always be 360°, then each exterior angle would be 60° (360° ÷ 6 = 60°).
The sum of the exterior angles of any polygon is 360o. The sum of exterior angles formula claims the amount of all exterior angles in any polygon is 360°. How do you find the sum of the exterior angles of a hexagon? If each of the remaining exterior angles is x°, find the value of x. And what we had to do is figure out the sum of the particular exterior angles of the hexagon. By using the sum of exterior angles formula, prove that each interior angle and its corresponding exterior angle in any polygon are supplementary.
Another Article :

As it is a regular hexagon, each angle is the same, thus each. By using the sum of exterior angles formula, prove that each interior angle and its corresponding exterior angle in any polygon are supplementary. However, to determine the exterior angle measures of an irregular hexagon, we need to use other methods. As it is a regular hexagon, each angle is the same, thus each. Each interior angle of a regular hexagon has a measure of 120°. Theorem Sum of the Exterior Angles of a Convex Polygon.

Ni is number of sides of a polygon. Sum of the measures of angles of a polygon: There are six angles, so 720 ÷ 6 = 120°. Solved examples on sum of exterior angles formula. By learning the theorems you can solve different types of problems in exams. Chapter 7 Class Notes.

360 / n =360 / 6 =60 degrees how many degrees in a heptagon? These angles have a total sum of 360°. A polygon whose all sides. In a regular hexagon, all sides are same size and measure of all interior angles are same. The measure of each exterior angle is 360°/n; sum of exterior angles of a polygon part 2 YouTube.

A regular hexagon has 6 equal exterior and 6 equal interior angles. Together, the adjacent interior and exterior angles will add to 180° 180 °. So it would�ve been this angle, we should call a, this angle b, c, d, and e. 360 / n =360 / 6 =60 degrees how many degrees in a heptagon? To find the value of a given exterior angle of a regular polygon, simply divide 360 by the number of sides or angles that the polygon has. POLYGONS Mind42.

To find the sum of the interior angles of a hexagon, divide it up into triangles. The formula used for finding the measure of interior angle of a polygon is given as: A polygon whose all sides. The measure of each exterior angle of a regular hexagon. A rule of polygons is that the sum of the exterior angles always equals 360 degrees. Interior Angles Of A Hexagon Home Designs.
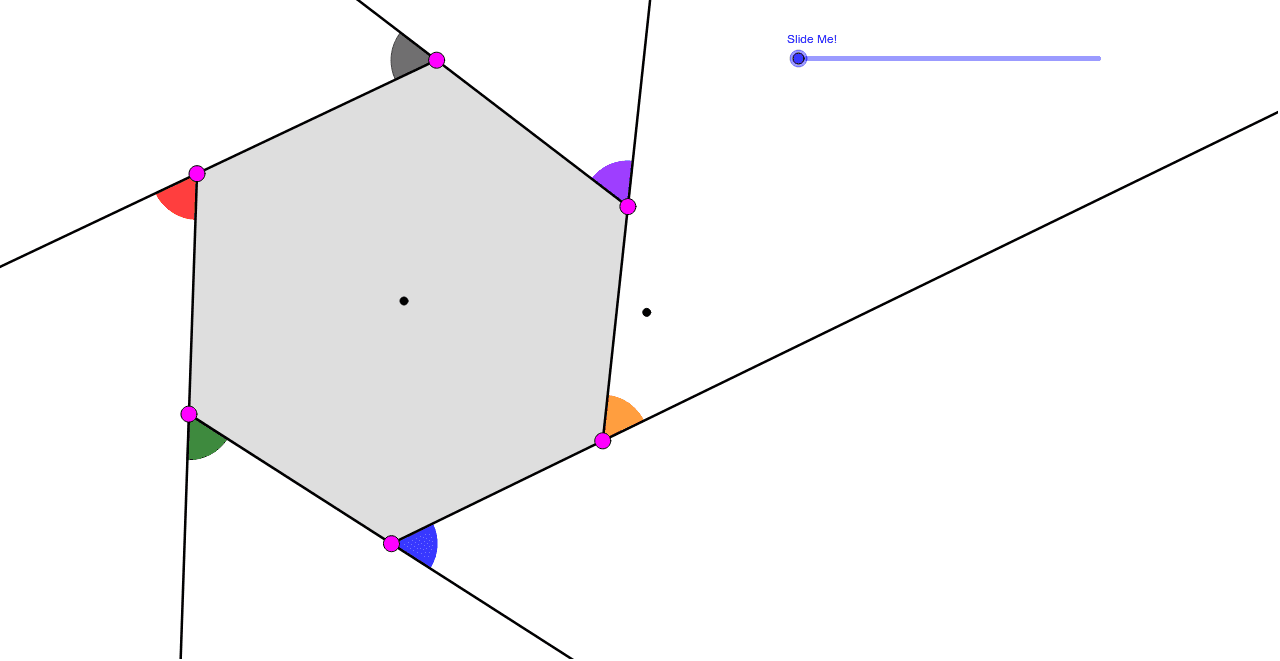
These angles have a total sum of 360°. The exterior angles of a hexagon are the angles formed when we extend the sides of the hexagon. As always, the sum of the exterior angles is 360 degrees. The sum of the exterior angles of a regular polygon will always equal 360 degrees. If each of the remaining exterior angles is x°, find the value of x. 34+ Hexagon Angles Exterior Pics OCSA.
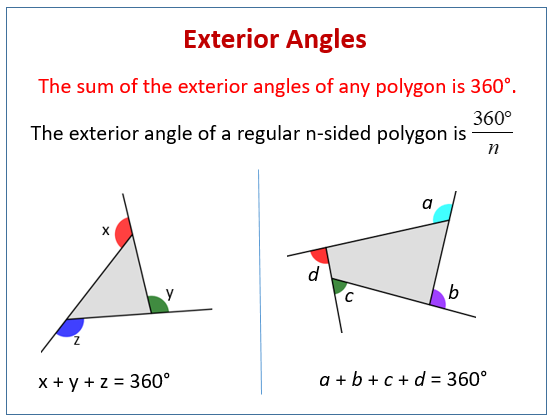
Each interior angle of a regular hexagon has a measure of 120°. Subsequently, question is, why is the sum of the exterior angles of any polygon 360? To find the sum of the interior angles of a hexagon, divide it up into triangles. By learning the theorems you can solve different types of problems in exams. Exterior angle = θ = 360 / n. Exterior Angles of Polygons (examples, solutions, videos.
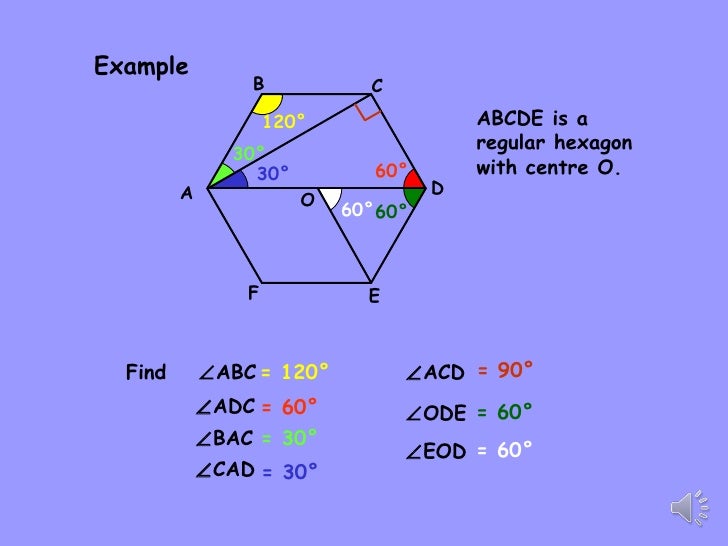
Sum of the exterior angles of a hexagon. If the hexagon is regular, we can simply divide the sum by 6 to get the measure of each exterior angle. So it would�ve been this angle, we should call a, this angle b, c, d, and e. The sum always holds regardless of whether the hexagon is regular or irregular. We know that number of sides = sum of exterior angles / each exterior angle = 360° / 30°= 12 thus the regular polygon has 12 sides. POLYGON PROPERTIES 9B.

Sum of the interior angles of a hexagon: To find the value of a given exterior angle of a regular polygon, simply divide 360 by the number of sides or angles that the polygon has. Sum of the interior angles of a hexagon: The sum of interior angles of a hexagon is 720^∘, which is double the sum of exterior angles. Sum of the exterior angles of a hexagon. How To Work Out The Interior Angle Of A Irregular Polygon.
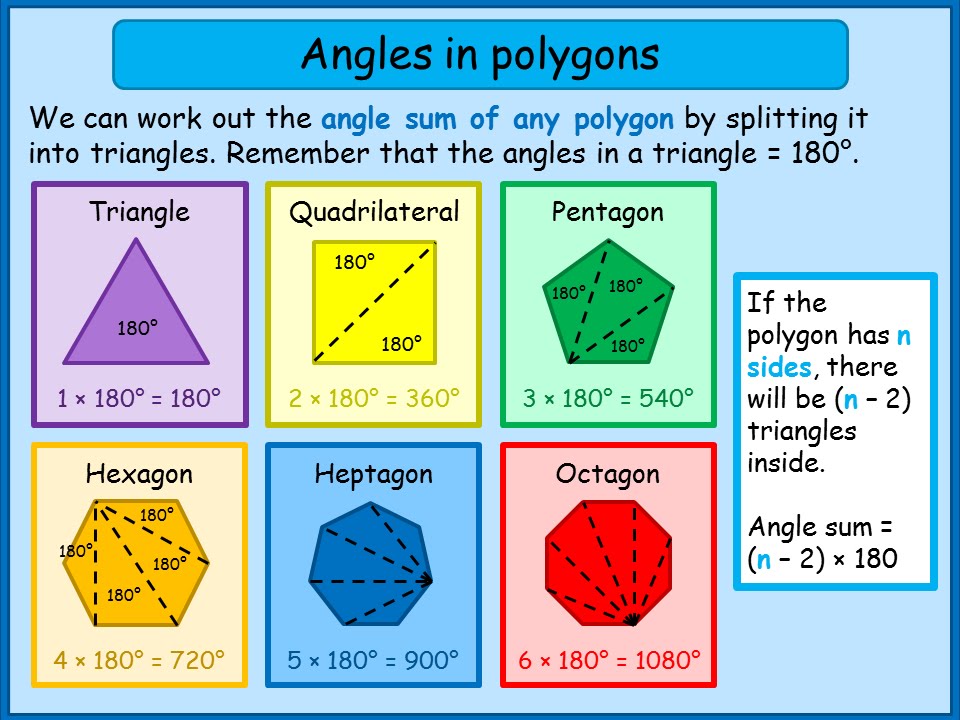
So, the value of d or interior angle is 120 degrees. The measure of each individual angle in a regular hexagon can be determined by dividing the sum by 6. We know that number of sides = sum of exterior angles / each exterior angle = 360° / 30°= 12 thus the regular polygon has 12 sides. To find the sum of the interior angles of a hexagon, divide it up into triangles. To find the value of a given exterior angle of a regular polygon, simply divide 360 by the number of sides or angles that the polygon has. Angle sum of any polygon Maths Tutorials YouTube.
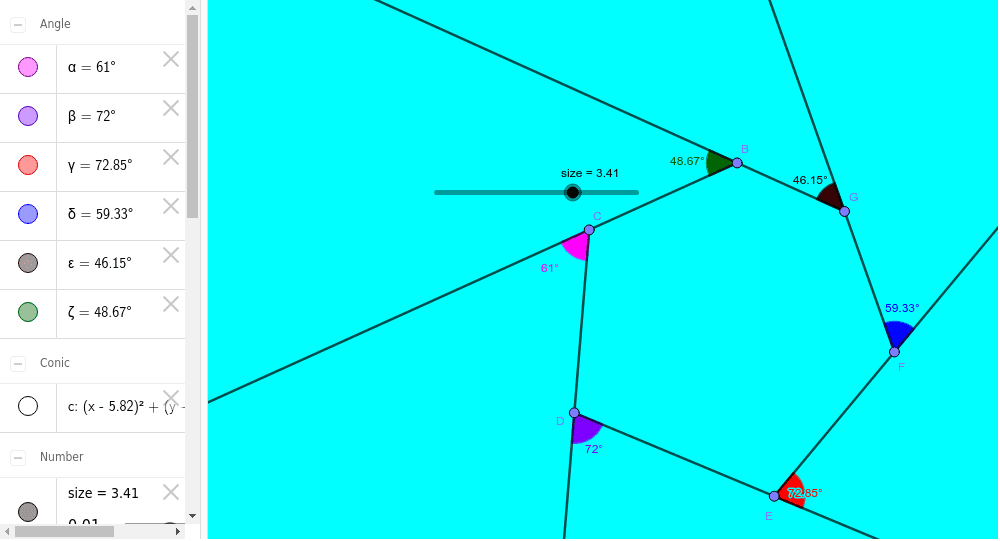
Ni is number of sides of a polygon. A rule of polygons is that the sum of the exterior angles always equals 360 degrees. Find the angle of each exterior angle of the hexagon to find the sum of the exterior angles of the hexagon. From the above triangle, the exterior angle y and r comprise a linear pair.(y + r = 180°). For a square, the exterior angle is 90° 90 °. Sum of Exterior Angles GeoGebra.

Given that, the measure of an exterior angle=60 the sum of all the exterior angles of the regular polygon = 360° Subsequently, question is, why is the sum of the exterior angles of any polygon 360? The sum of the exterior angles of a regular polygon will always equal 360 degrees. If the hexagon is regular, we can simply divide the sum by 6 to get the measure of each exterior angle. D=180 (n−1)n, “d” represents interior angle and n is the number of sides in the polygon. Sum of Exterior Angles of Polygons (Property) Teachoo.

Each interior angle of a regular hexagon has a measure of 120°. Together, the adjacent interior and exterior angles will add to 180° 180 °. To find the sum of the interior angles of a hexagon, divide it up into triangles. If the hexagon is regular, we can simply divide the sum by 6 to get the measure of each exterior angle. True the sum of exterior angles of a hexagon is 360^∘. Sum of exterior angles in a polygonPart 1 YouTube.
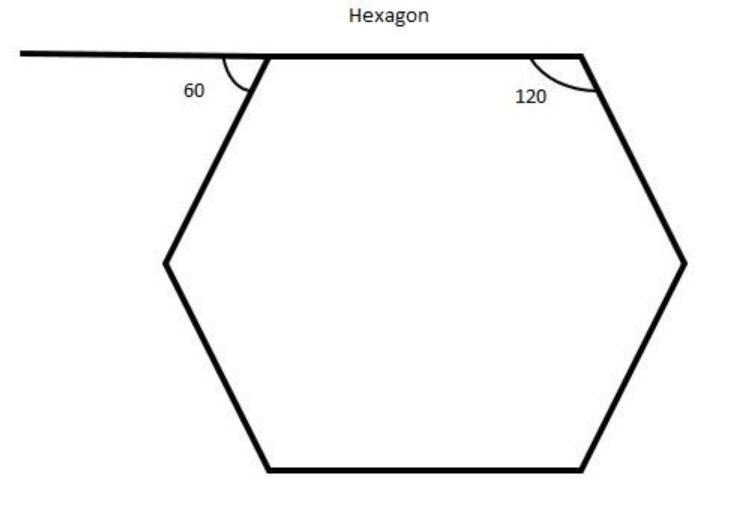
What is exterior angle of a hexagon? Sum of exterior angles of a polygon is ∠a’ + ∠b’ + ∠c’ +. The sum always holds regardless of whether the hexagon is regular or irregular. True the sum of exterior angles of a hexagon is 360^∘. And what we had to do is figure out the sum of the particular exterior angles of the hexagon. The sum of the exterior angles of a hexagon is A 3600.
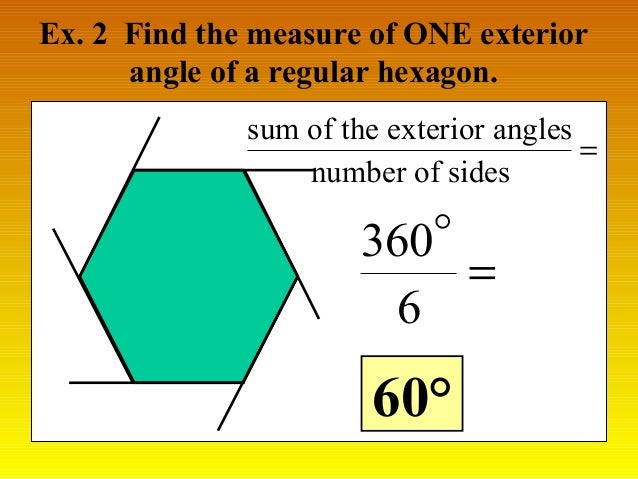
The formula used for finding the measure of interior angle of a polygon is given as: If the hexagon is regular, we can simply divide the sum by 6 to get the measure of each exterior angle. The total sum of all the interior angles of a hexagon equals 720°. Hint:first of all, find the sum of interior angles of the hexagon and so that we can find each interior angle. Because the sum of these angles will always be 360°, then each exterior angle would be 60° (360° ÷ 6 = 60°). Naming anglesofpolygons.