This means we can divide 360 360 360 360 by 8 8 8 8 to get the solution. The exterior angles of a polygon when added gives a total of 360°. exterior of a regular polygon.
Exterior Of A Regular Polygon, Although you know that sum of the exterior angles is 360, you can only use formula to find a single exterior angle if the polygon is regular! So each exterior angle is 360 divided by the n, the number of sides. To find the value of a given exterior angle of a regular polygon, simply divide 360 by the number of sides or angles that the polygon has.
 Interior Angles of Regular Polygons A Plus Topper From aplustopper.com
Interior Angles of Regular Polygons A Plus Topper From aplustopper.com
Sum of exterior and interior angles is 180 deg. By the exterior angle formula, the sum of the exterior angles in any polygon is 360°. You will see that the angles combine to a full 360° circle.
As a demonstration of this, drag any vertex towards the center of the polygon.
Anyway, we can name the number of sides s and the number of angles a. Interior angles of a regular polygon How many sides does the polygon have? You will see that the angles combine to a full 360° circle. Sum of exterior and interior angles is 180 deg. The sum of the exterior angles of a polygon is 360°.
Another Article :

Sum of exterior and interior angles is 180 deg. Even though we know that all the exterior angles add up to 360 °, we can see, by just looking, that each $$ \angle a \text{ and } and \angle b $$ are not congruent. The exterior angles of a polygon when added gives a total of 360°. Exterior angle of polygon = 360 ° ÷ number of sides = 360 ° /n Some of the regular polygons along with their names are given below: Pin by Khelvinjit Singh on Woodwork Syllabus Math.

The measure of each exterior angle of a regular polygon = 360 o n = 360 o 10 = 36 o hence, the measure of each exterior angle of a decagon is. What is the formula for finding interior angles of a polygon? Exterior angles of a polygon are formed when by one of its side and extending the other side. The measure of each exterior angle of a regular polygon = 360 o n = 360 o 10 = 36 o hence, the measure of each exterior angle of a decagon is. If the interior angle is 3x, the exterior angle is x. Exterior Angles of Regular Polygons Worksheet EdPlace.
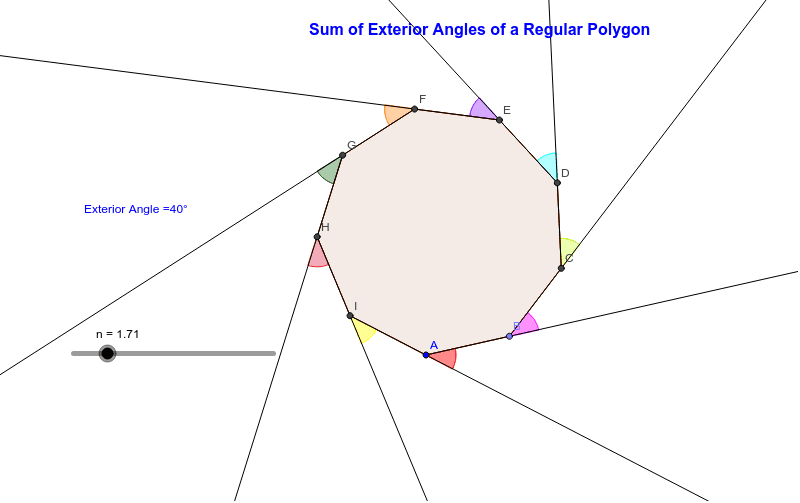
360°÷5 = 72° each exterior angle of a regular pentagon measures 72°. If the polygon was not regular, the exterior angles could be 30°, 170°, and 160°! This means we can divide 360 360 360 360 by 8 8 8 8 to get the solution. A regular octagon has 8 8 8 8 interior angles equal in size, so the eight exterior angles are equal. Consider, for instance, the pentagon pictured below. Exterior Angles of a Regular Polygon Demonstration GeoGebra.
A polygon is a flat figure that is made. Since the polygon is regular, the measure of all the interior angles needs to be the same. A polygon that has six sides is known as a hexagon. This means we can divide 360 360 360 360 by 8 8 8 8 to get the solution. Exterior angle of a regular polygon = 360°/n, here n =10 = 360°/10 = 36° central angle the central angle of a polygon is the angle formed at the center of the polygon by any two adjacent vertices. Exterior Angles of Regular Polygons Formula with.
Thus the regular polygon has 12 sides. Interior angles of a regular polygon As a demonstration of this, drag any vertex towards the center of the polygon. A regular octagon has 8 8 8 8 interior angles equal in size, so the eight exterior angles are equal. A polygon that has six sides is known as a hexagon. Find missing exterior angles of polygons.
How many sides does the polygon have? The number of central angles in a polygon is. Exterior angles of a polygon add up to 360 360 360 360. The sum of all the exterior angles in a polygon is equal to 360 degrees. The sum total of these angles is always equal to 360°. Find missing exterior angles of polygons.
Now, we know that sum of exterior angles of a regular polygon is 360 ° the formula to calculate the measure of an exterior angle is: Calculating the size of each exterior angle of regular polygons the formula for calculating the size of an exterior angle of a regular polygon. We know that for a regular polygon the exterior angle of any side is equal to [{{360}^{\circ }}\div \theta =n], we can substitute the given exterior angle in this formula to find the number of sides. Exterior angles of a polygon add up to 360 360 360 360. Although you know that sum of the exterior angles is 360, you can only use formula to find a single exterior angle if the polygon is regular! 30+ What Is The Measure Of Each Exterior Angle Of A.

The exterior angle and its corresponding interior angle in a polygon are supplementary (i.e their sum is equal to 180°) in a regular polygon, all the exterior angles have the same values. As a demonstration of this, drag any vertex towards the center of the polygon. To find the value of a given exterior angle of a regular polygon, simply divide 360 by the number of sides or angles that the polygon has. The exterior angle of a regular pentagon = 360 ∘ 5 = 72 ∘ regular hexagon: Interior angles of a regular polygon Interior Angles of Regular Polygons YouTube.

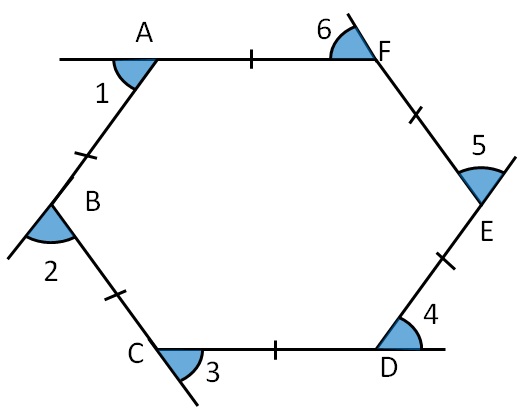
We can see that all the exterior angles of a polygon have a total sum of 360°. A polygon that has six sides is known as a hexagon. Exterior angles of a regular polygon exterior angles of every simple polygon add up to 360o, because a trip around the polygon completes a rotation, or return to your starting place. How many sides does the polygon have? The number of central angles in a polygon is. Regular Polygon Definition, Examples and Properties Cuemath.

Exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides is calculated using exterior_angle = (2* pi)/ number of sides.to calculate exterior angle of regular polygon, you need number of sides (n sides).with our tool, you need to enter the respective value for number of sides and hit the calculate button. Of course, for a polygon that is not regular, we would need to do a little more work to find the measure of an individual interior angle. The measure of each exterior angle of a regular polygon = 360 o n = 360 o 10 = 36 o hence, the measure of each exterior angle of a decagon is. A polygon that has six sides is known as a hexagon. Since the polygon is regular, the measure of all the interior angles needs to be the same. Polygon Shape Cuemath.

Sum of exterior and interior angles is 180 deg. Therefore, we can calculate the measure of one of the exterior angles of a regular polygon by dividing 360° by the number of sides of the regular polygon. How many sides does the polygon have? The measure of each exterior angle of a regular polygon = 360 o n = 360 o 10 = 36 o hence, the measure of each exterior angle of a decagon is. To find the value of a given exterior angle of a regular polygon, simply divide 360 by the number of sides or angles that the polygon has. Exterior Angles of Regular Polygons YouTube.

Consider, for instance, the pentagon pictured below. Sum of exterior and interior angles is 180 deg. This means we can divide 360 360 360 360 by 8 8 8 8 to get the solution. So the polygon has 360/45 = 8 sides or it is a regular octagon. Therefore, we can calculate the measure of one of the exterior angles of a regular polygon by dividing 360° by the number of sides of the regular polygon. Angles, areas and diagonals of regular polygons.

Since the polygon is regular, all the angles are congruent. Given that, the measure of an exterior angle=60 the sum of all the exterior angles of the regular polygon = 360° let the number of sides be = n. We know that for a regular polygon the exterior angle of any side is equal to [{{360}^{\circ }}\div \theta =n], we can substitute the given exterior angle in this formula to find the number of sides. A regular octagon has 8 8 8 8 interior angles equal in size, so the eight exterior angles are equal. If the interior angle is 3x, the exterior angle is x. Regular Polygon Definition, Examples and Properties Cuemath.

For example, for a pentagon, we have: How many sides does the polygon have? Hence, all its exterior angles are to be measured in the same as well, i.e., 60 degrees. We know that for a regular polygon the exterior angle of any side is equal to [{{360}^{\circ }}\div \theta =n], we can substitute the given exterior angle in this formula to find the number of sides. Exterior angle of a regular polygon = 360°/n, here n =10 = 360°/10 = 36° central angle the central angle of a polygon is the angle formed at the center of the polygon by any two adjacent vertices. Interior Angles of Regular Polygons A Plus Topper.

Some of the regular polygons along with their names are given below: If the polygon was not regular, the exterior angles could be 30°, 170°, and 160°! If the interior angle is 3x, the exterior angle is x. The sum of all the exterior angles in a polygon is equal to 360 degrees. Since the polygon is regular, all the angles are congruent. Regular Polygon Definition, Examples and Properties Cuemath.










