An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle. If an exterior angle of a triangle is bisected, the bisector divides the opposite side externally into segments whose lengths are in the same ratio as the lengths of the other sides of the triangle. exterior angle bisector theorem of a triangle.
Exterior Angle Bisector Theorem Of A Triangle, B d c ^ = π − b i c ^ = a b c ^ + a c b ^ 2 = π − b a c ^ 2. Angle bisector a d cuts. The interior angle bisector theorem:
 External Bisector of angle of triangle divides opposite From youtube.com
External Bisector of angle of triangle divides opposite From youtube.com
The bisector of the exterior angle at b and the bisector of ∠c intersect each other at d. Prove that ∠d = 1 2 ∠a. 6 (12 + op) = 10 op.
If an angle of a triangle is bisected internally or externally by a straight line which cuts the opposite side or the opposite side produced, the segments of that side will have the same ratio as the other sides of the triangle;
Every triangle has six exterior angles (two at each vertex are equal in measure). The exterior angles, taken one at each vertex, always sum up to 360°. The angle bisector is nothing but a line or line segment which divides the angle into two equal parts. External angle bisector theorem : 6 (12 + op) = 10 op. If the external bisector of an angle.
Another Article :

According to the external angle theorem, when a triangle’s side is stretched, the resulting exterior angle is equal to the sum of the measurements of the triangle’s two opposed internal angles. Is the following figure of a triangle correct. Triangle angle bisector theorem states that in a triangle, the angle bisector of any angle will divide the opposite side in the ratio of the sides containing the angle. An angle bisector of a triangle divides the interior angle�s opposite side into two segments that are proportional to the other two sides of the triangle. External angle bisector theorem : Lesson Video Angle Bisector Theorem and Its Converse Nagwa.

Theorem the internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding. Angle bisector a d cuts. The bisector of the exterior angle at b and the bisector of ∠c intersect each other at d. X x x 57 43 50 x 53 62 80 65 x 80 50 44 x title. See 7 best images of exterior angles of a triangle worksheet. prove that the external bisectors of an angle of a.
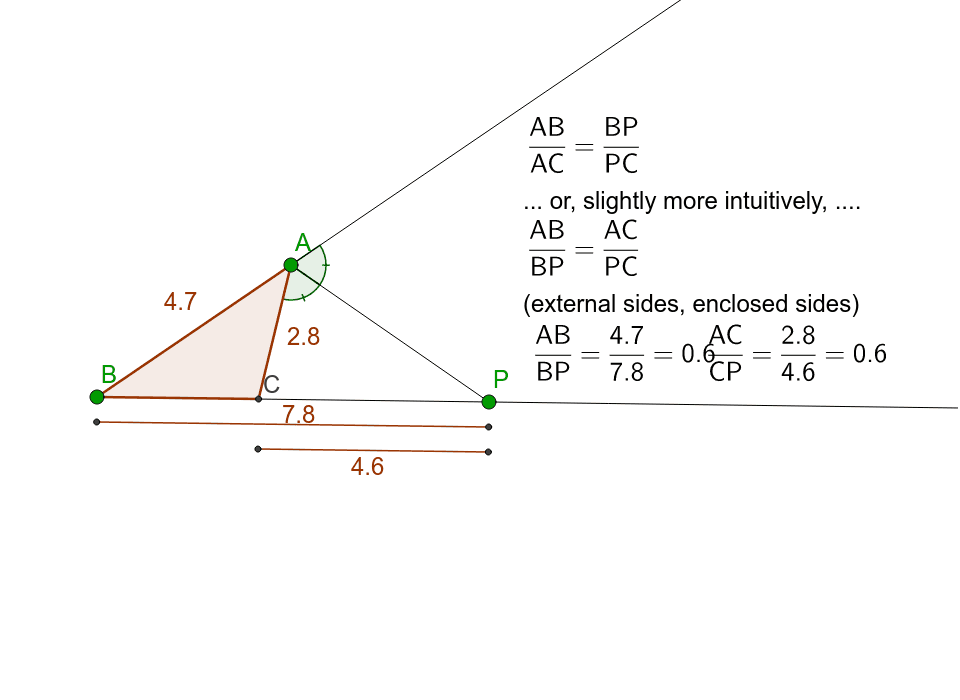
If ad is (internal) angle bisector meeting side bc at d in a triangle abc, ab/ac = bd/cd. Inspiring exterior angles of a triangle worksheet worksheet images. If an angle of a triangle is bisected internally or externally by a straight line which cuts the opposite side or the opposite side produced, the segments of that side will have the same ratio as the other sides of the triangle; 6 (12 + op) = 10 op. The exterior angle theorem tells us that any exterior angle of a triangle equals the sum of the opposite two interior angles and that the sum of all three interior angles of a triangle equals 180° 180 °, the sum of two right angles (triangle sum theorem). Angle bisector theorem (external) GeoGebra.
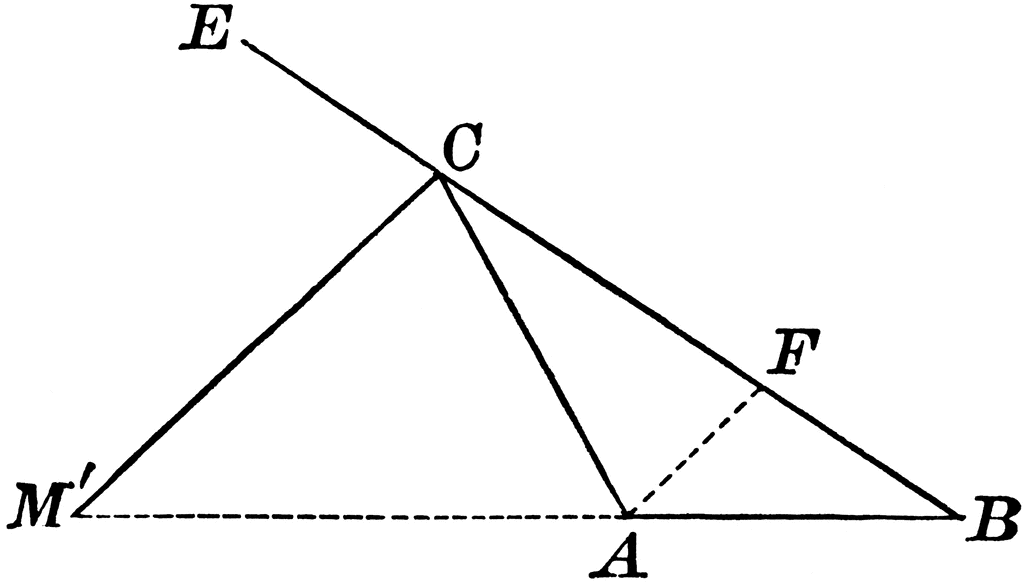
Draw b e ↔ ∥ a d ↔. That is, if ad is the angle bisector of angle a in triangle abc, open gsp file for theorem 4.7 and its proof. The angle bisector is nothing but a line or line segment which divides the angle into two equal parts. If the external bisector of an angle. X x x 57 43 50 x 53 62 80 65 x 80 50 44 x title. Exterior Angle Bisector of Triangle Dividing Opposite Side.
Now, we need to prove that the external bisector of an angle of a. The angle bisector theorem is defined for internal angles and also external angles. By the angle bisector theorem, b d d c = a b a c proof: The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle�s side is divided into by a line that bisects the opposite angle. The angles created between the side of the polygon and the extended adjacent side of the polygon are known as exterior angles. Exterior Angle Bisector of Triangle Dividing Opposite Side.

The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. Angle bisector a d cuts. X x x 57 43 50 x 53 62 80 65 x 80 50 44 x title. Is the following figure of a triangle correct. Inspiring exterior angles of a triangle worksheet worksheet images. Angle Bisector of Triangle Definition, Theorem, Proof.

An angle bisector of a triangle divides the interior angle�s opposite side into two segments that are proportional to the other two sides of the triangle. The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. If ad is (internal) angle bisector meeting side bc at d in a triangle abc, ab/ac = bd/cd. External angle bisector theorem : Bd dc = ab ac bd dc = ab ac. Math 8 Chapter 3 Lesson 3 Properties of the bisector of a.

If ad is (internal) angle bisector meeting side bc at d in a triangle abc, ab/ac = bd/cd. Prove that ∠d = 1 2 ∠a. If the external bisector of an angle. If ad is (internal) angle bisector meeting side bc at d in a triangle abc, ab/ac = bd/cd. Exterior angle bisector theorem : Prove that the angle formed by the bisector of interior.

That is, if ad� is the angle bisector of the external angle at a in triangle abc, then An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle. Angle bisector a d cuts. Mp is the external bisector of angle m by using angle bisector theorem in the triangle mno we get, (np/op) = (mn/mo) np = no + op = 12 + op (12 + op)/op = 10/6. The bisector of the exterior angle at b and the bisector of ∠c intersect each other at d. External Angle bisector Theorem of triangle External.
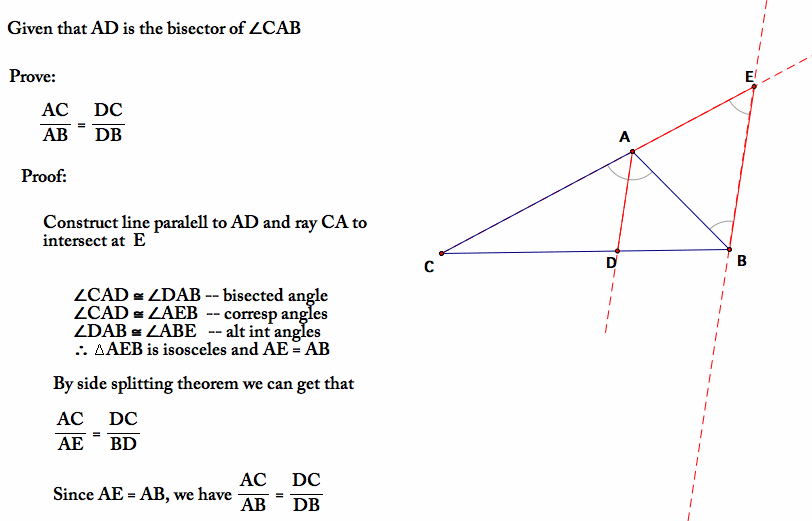
The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. Theorem the internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding. (ii) if d0 2 bcn[bc], then [ad0 is the external bisector of angle a if and only if d0b d0c = ab ac. Where [ad, [ad0 are the lengths of internal, respectively external bisector of the angle a and d;d0 2 bc. And, if a side of a triangle be divided internally or externally so that its segments have the same ratio as the other sides of the triangle, the straight line drawn from. Section 4.2 Discussion.

- in the given figure, ae is the bisector of the exterior ∠cad meeting bc produced in e. See 7 best images of exterior angles of a triangle worksheet. By the angle bisector theorem, b d d c = a b a c proof: Angle bisector a d cuts. Where [ad, [ad0 are the lengths of internal, respectively external bisector of the angle a and d;d0 2 bc. Teorema de la bisectriz de ángulo Angle bisector theorem.

That is, if ad is the angle bisector of angle a in triangle abc, open gsp file for theorem 4.7 and its proof. In a triangle, the angle between the inner bisector of the same corner and the outer bisector is 90 degrees, and the ratio between the parts separated by the inner bisector and the outer bisector is equal to the distance of the outer bisector to the other corners. This is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate. X x x 57 43 50 x 53 62 80 65 x 80 50 44 x title. That is, if ad� is the angle bisector of the external angle at a in triangle abc, then Exterior angle bisector theorem proof YouTube.
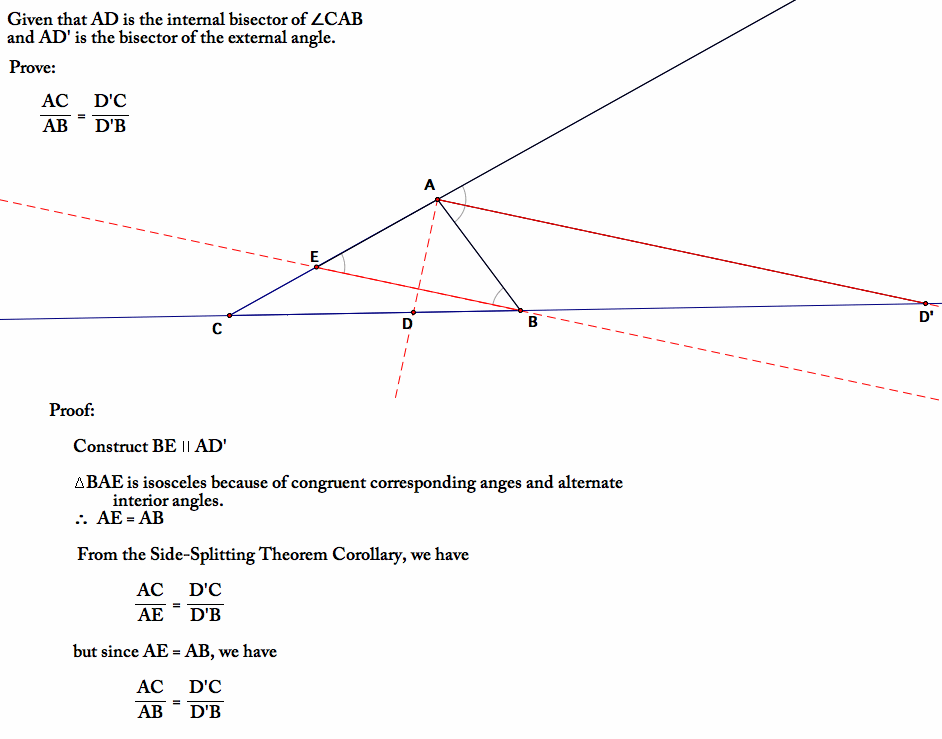
The easy method to remember the angle bisector theorem of a triangle is. The exterior angle bisectors are just orthogonal to the interior angle bisectors, hence. If an exterior angle of a triangle is bisected, the bisector divides the opposite side externally into segments whose lengths are in the same ratio as the lengths of the other sides of the triangle. The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. That is, if ad is the angle bisector of angle a in triangle abc, open gsp file for theorem 4.7 and its proof. Section 4.2 Discussion.

According to the external angle theorem, when a triangle’s side is stretched, the resulting exterior angle is equal to the sum of the measurements of the triangle’s two opposed internal angles. The exterior angle theorem is proposition 1.16 in euclid�s elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. The angles created between the side of the polygon and the extended adjacent side of the polygon are known as exterior angles. The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. The internal angle bisector of an angle of a triangle.

Prove that ∠d = 1 2 ∠a. The angle bisector is nothing but a line or line segment which divides the angle into two equal parts. If an angle of a triangle is bisected internally or externally by a straight line which cuts the opposite side or the opposite side produced, the segments of that side will have the same ratio as the other sides of the triangle; In a triangle, the angle between the inner bisector of the same corner and the outer bisector is 90 degrees, and the ratio between the parts separated by the inner bisector and the outer bisector is equal to the distance of the outer bisector to the other corners. I.e., the angle bisector formula is: Internal Angle Bisector Theorem of Triangle Internal.










