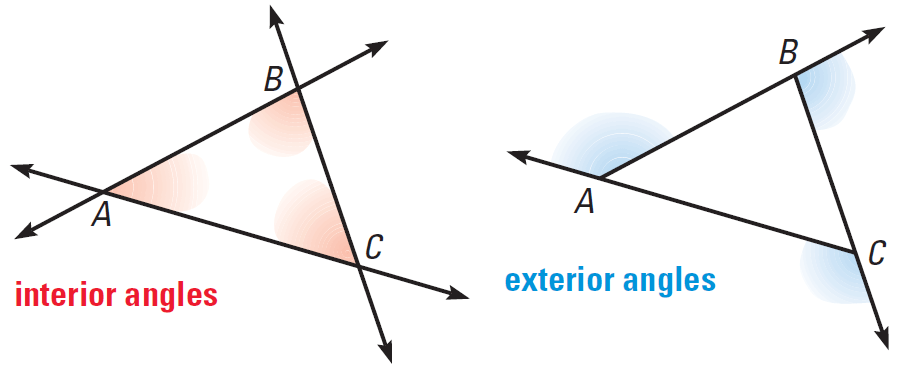
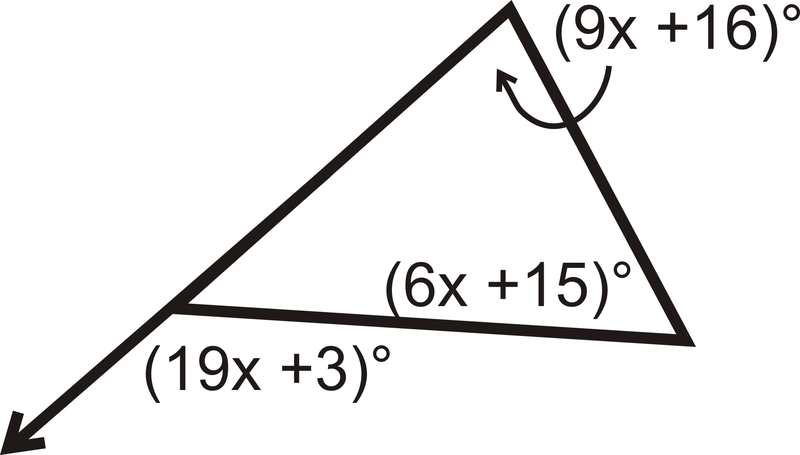Every triangle has six exterior angles (two at each vertex are equal in measure). All the angles of a triangle can be less than all the angles of a triangle can be greater than all the angles of a triangle can be equal to a triangle can have two obtuse angles. a triangle with two acute exterior angles.
A Triangle With Two Acute Exterior Angles, A right triangle can, and must, have exactly two acute angles. Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. Textbook solution for mcdougal littell jurgensen geometry:

Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. As a right triangle has one angle equal to 90∘, this means the sum of the remaining two angles must be 180∘ −90∘ = 90∘. Since a triangle�s angles must sum to 180° in euclidean geometry, no euclidean triangle can have more than one obtuse angle.
The exterior angle of a triangle is equal to the sum of the interior angles of the triangle.
Exterior angle = sum of two opposite interior angles if exterior angle is acute (<90degree) that means sum of two angles of traingle is less than 90, there third angle would have to be above 90 degree otherwise traingles wouldn�t be possible as sum of all angles of traingle is 180 advertisement answer 3.8 /5 16 brainly user advertisement Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. To see this, just remember that the sum of the angles of a triangle must be 180∘. All acute triangles have three acute angles. Otherwise, a triangle always has 2 obtuse exterior angles and 1 acute exterior. Therefore at least two angles have to be acute since that is the only scenario (besides having 3 acute angle) for a triangle to form.
Another Article :

Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. (iii) if an exterior angle of a triangle is a right angle, then each of its interior opposite angles is acute. Every triangle has six exterior angles (two at each vertex are equal in measure). You need to fi nd the measure of each acute angle. Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. Notes on Triangle Grade 9 > Compulsory Maths > Geometry.
[2] the pattern is that the exterior angle is the same size as the sum of the 2 angles. So, every triangle needs to have at least 2 acute angles. A right triangle can, and must, have exactly two acute angles. An exterior angle is supplementary to its adjacent triangle interior angle. Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. Triangle Sum and Exterior Angle Theorems CK12 Foundation.
The exterior angle sharing the same side with that of the right angle of the triangle is equal to 90°. An acute exterior angle means that it�s supplement is greater than 90 degrees. All acute triangles have three acute angles. Every triangle will have atleast two acute angles, each < 90°. Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. Using angle measures in triangles.

All the angles of a triangle can be less than all the angles of a triangle can be greater than all the angles of a triangle can be equal to a triangle can have two obtuse angles. The exterior angle sharing the same side with that of the right angle of the triangle is equal to 90°. In this figure the interior angle of the triangle is two acute angles and an obtuse angle. That will be one of the interior angles of the triangle. (vi) every equilateral triangle is an isosceles triangle. Exterior Angles of a Triangle & Exterior Angle Theorem.mov.
That will be one of the interior angles of the triangle. (iii) if an exterior angle of a triangle is a right angle, then each of its interior opposite angles is acute. Using the exterior angle property of triangles, find the value of the exterior angle indicated in the picture below. A triangle can have at most one obtuse angles. Make a plan first, sketch a diagram of the situation. Using angle measures in triangles.
![Properties of Triangle types & formulas [Video & Practice] Properties of Triangle types & formulas [Video & Practice]](https://cdn.e-gmat.com/blogs/wp-content/uploads/2019/07/Properties-of-triangle-Acute-angled-triangle-1024x518.png)
(vi) every equilateral triangle is an isosceles triangle. [2] the pattern is that the exterior angle is the same size as the sum of the 2 angles. Only in the case of an equilateral triangle. Therefore at least two angles have to be acute since that is the only scenario (besides having 3 acute angle) for a triangle to form. If the other exterior angles are 13x and 14x then, they add up to 270°. Properties of Triangle types & formulas [Video & Practice].
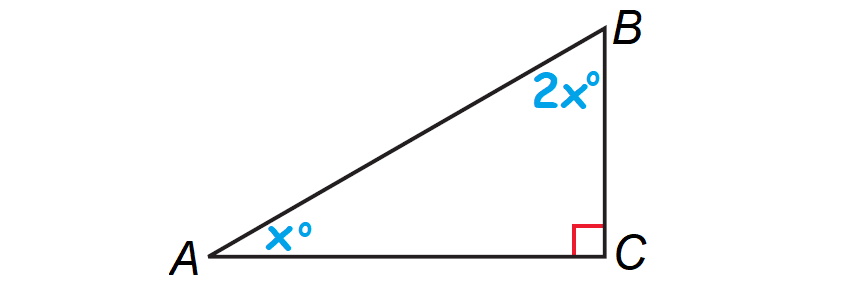
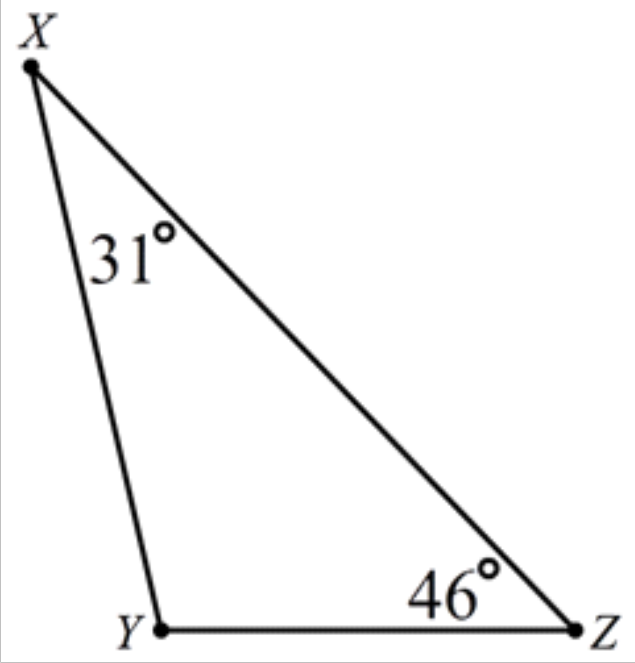
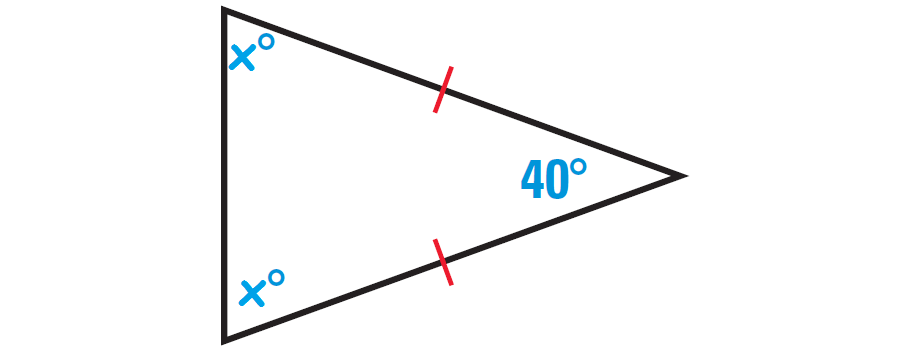
Find measure ∠a and ∠c m∠a + m∠b+m∠c =180° 36 + x + (x + 4) = 180 40 + 2x = 180 2x = 140 x = 70 = m∠a All the angles of a triangle can be less than all the angles of a triangle can be greater than all the angles of a triangle can be equal to a triangle can have two obtuse angles. Such a triangle does not exist because it would mean that the sum of the angles of the triangle are more than 180 degrees, a violation of the property of triangles that the sum of the angles equal 180 degrees. There is no way that one of these angles can be greater than 90 degees, and If the other exterior angles are 13x and 14x then, they add up to 270°. Triangles and Angles Worksheet.
Such a triangle does not exist because it would mean that the sum of the angles of the triangle are more than 180 degrees, a violation of the property of triangles that the sum of the angles equal 180 degrees. Textbook solution for mcdougal littell jurgensen geometry: Therefore at least two angles have to be acute since that is the only scenario (besides having 3 acute angle) for a triangle to form. You can use the corollary to the triangle sum theorem and the given relationship between the two acute angles to write and solve an equation to fi nd the measure of each acute angle. Since the interior angles add up to 180 degrees, that means the remaining 2 interior angles must add up to less than 90 degrees. Triangle Sums CK12 Foundation.

Therefore at least two angles have to be acute since that is the only scenario (besides having 3 acute angle) for a triangle to form. Otherwise, a triangle always has 2 obtuse exterior angles and 1 acute exterior. A triangle can never have only one acute angle. The triangle can have more than one exterior angles that can be acute or obtuse angles since the triangles angles must sum to 180 degrees. [2] the pattern is that the exterior angle is the same size as the sum of the 2 angles. PPT 7.2 Exterior Angle Theorem PowerPoint Presentation.
In this figure the interior angle of the triangle is two acute angles and an obtuse angle. A right triangle can, and must, have exactly two acute angles. Since a triangle’s angles must sum to 180° in euclidean geometry, no euclidean triangle can have more than one obtuse angle.acute and obtuse triangles are the two different types of oblique triangles — triangles that are not right triangles because they have no. Every triangle has six exterior angles (two at each vertex are equal in measure). (vi) every equilateral triangle is an isosceles triangle. Triangle Sum and Exterior Angle Theorems CK12 Foundation.

An exterior angle is supplementary to its adjacent triangle interior angle. Find measure ∠a and ∠c m∠a + m∠b+m∠c =180° 36 + x + (x + 4) = 180 40 + 2x = 180 2x = 140 x = 70 = m∠a Because consider the fact that if we have an acute exterior angle, for example, say this is 30 degrees and then we know this adds upto 1 80 then this would have to be 100 50 degrees. Student edition… 5th edition ray c. In two dimensional space, a triangle with exactly one acute angle means that the other two angles are right or obtuse. How to find an angle in an acute / obtuse triangle SSAT.
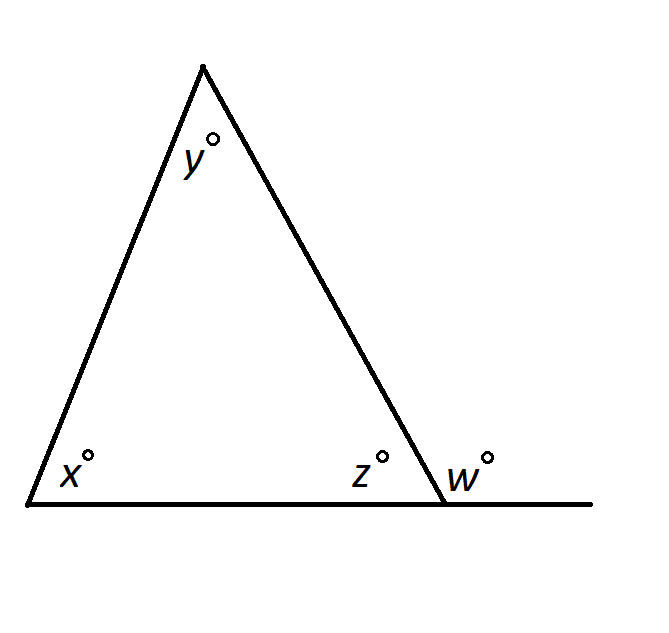
Using the exterior angle property of triangles, find the value of the exterior angle indicated in the picture below. Therefore at least two angles have to be acute since that is the only scenario (besides having 3 acute angle) for a triangle to form. Conversely, if the interior angle is acute then the exterior angle of the triangle will be obtuse. Only in the case of an equilateral triangle. Since the interior angles add up to 180 degrees, that means the remaining 2 interior angles must add up to less than 90 degrees. How to find an angle in an acute / obtuse triangle SSAT.
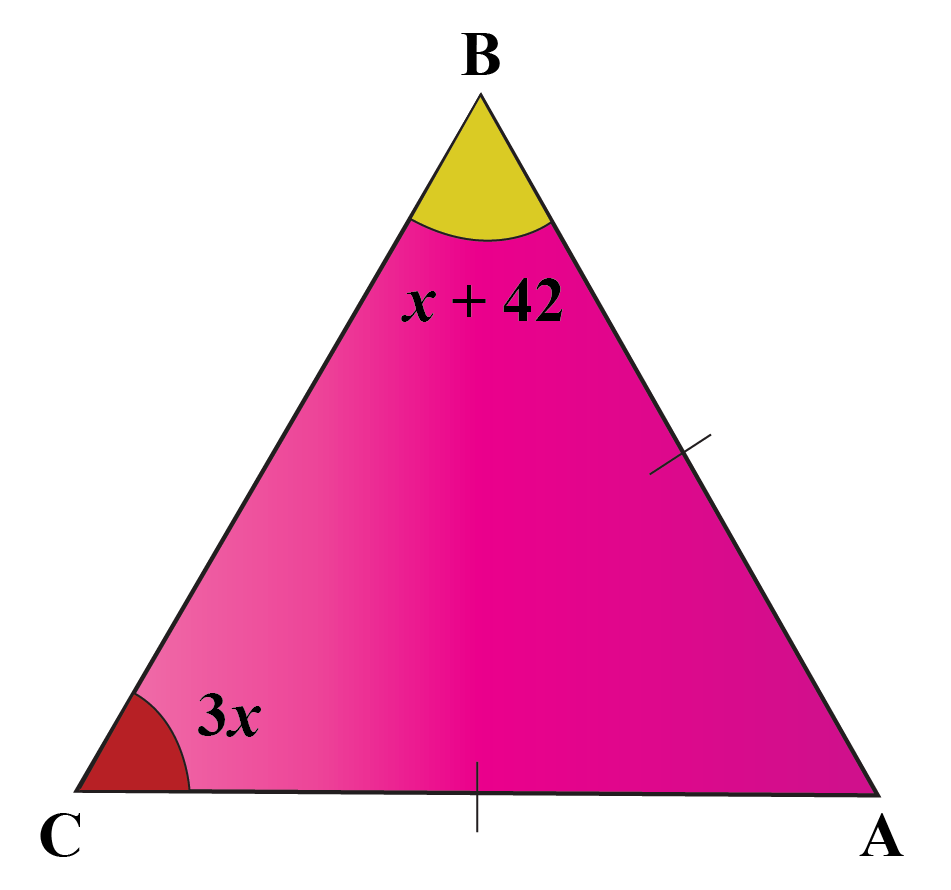
The exterior angles, taken one at each vertex, always sum up to 360°. Sum of the three angles of a triangle is a triangle can have two right angles. To see this, just remember that the sum of the angles of a triangle must be 180∘. It is not possible tohave a triangle with two cute exterior angles. All acute triangles have three acute angles. Acute triangle Definition, Formulas & Examples Cuemath.
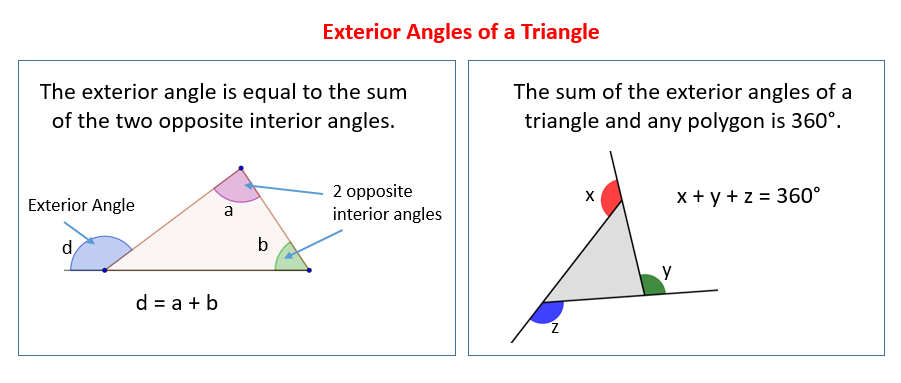
A triangle can have at most one obtuse angles. The equation that would allow us to determine the values of the angles are, 13x + 14x = 270 x = 10 the exterior angles are 130 and 140°. An exterior angle of a triangle is equal to the sum of the opposite interior angles. Conversely, if the interior angle is acute then the exterior angle of the triangle will be obtuse. (vi) every equilateral triangle is an isosceles triangle. Exterior Angles of a Triangle (solutions, examples, videos).
Since a triangle�s angles must sum to 180° in euclidean geometry, no euclidean triangle can have more than one obtuse angle. The sum of the angles of a triangle is 180°. An acute exterior angle means that it�s supplement is greater than 90 degrees. It is not possible tohave a triangle with two cute exterior angles. There is no way that one of these angles can be greater than 90 degees, and EXTERIOR ANGLE THEOREM (Part 1 Exploration).